Rendimiento de algoritmos y notación Big-O

En programación el rendimiento o la complejidad de un algoritmo se suele medir utilizando una notación denominada Big-O, y también conocida como Notación Asintótica o Notación Landau (en honor a uno de sus inventores, a  principios del siglo pasado, Edmund Landau).

Ya os hemos contado aquí la importancia que tiene aprender a crear ciertos algoritmos aunque no los vayas a usar en el día a día. Pero además, en cualquier documentación o en cualquier libro o página que describa un algoritmo nos vamos a encontrar con la notación Big-O, por lo que es muy importante conocerla. Por ejemplo, si consultamos la documentación de MSDN para la función RemoveAt de una SortedList nos dice qué es una operación O(n):

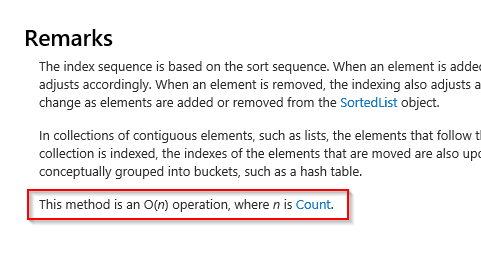
Nota: en general soy de los que opino que cualquier documentación técnica oficial es mucho mejor leerla en inglés, y éste es un buen ejemplo del porqué: en la versión en español de MSDN la notación Big-O aparece como "E/s(n)", que no tiene nada que ver, fruto de la traducción automática, que no va nada fina.

Y si consultamos el método Item para localizar o establecer un elemento en una colección de tipo ArrayList, nos dice que su complejidad es O(1).

¿Qué significa esto exactamente y por qué nos importa?

Vamos a verlo...

Entendiendo la notación Big-O

La notación Big-O nos proporciona una manera de saber cómo se va a comportar un algoritmo en función de los argumentos que le pasemos y la escala de los mismos.

Por ejemplo, imagínate una función que se utiliza para localizar un elemento dentro de una lista de elementos previamente guardados. Si la documentación de la misma nos dice que es una operación de tipo O(1), quiere decir que da igual cuántos elementos haya en la lista, la operación siempre tarda lo mismo. Para ser más exactos deberíamos decir que el esfuerzo de cómputo necesario es el mismo.

Por eso, por ejemplo, que en la documentación el indizador Item de un ArrayList que vimos antes, tenga complejidad O(1) quiere decir que da exactamente igual que la colección tenga uno o un millón de elementos: insertar o recuperar un elemento siempre tarda más o menos lo mismo.

Ahora supongamos que tenemos una función que dibuja en una gráfica los puntos que le pasemos en una matriz. Su documentación nos dice que su complejidad es O(n). Esto quiere decir, para entendernos, que si pintar 1 punto implica, por ejemplo, 10ms, pintar 2 implicaría 20ms, 3 puntos serían 30ms, etc... O sea, el tiempo necesario para ejecutar la función es función directa y lineal del número de elementos que le pasemos.

Es muy importante conocer el tipo de función/curva que se asocia con la ejecución de una función ya que nos permitirá saber de antemano si el rendimiento de nuestra aplicación se puede resentir en caso de que el tamaño de los datos a manejar aumente mucho. Así, entre dos algoritmos/funciones que hagan lo mismo, deberíamos elegir el que tenga una complejidad asintótica menor, para lo cual consultaremos la notación Big-O asociada al mismo.

Atendiendo a su complejidad, las notaciones Big-O más comunes para todo tipo de algoritmos y funciones son las que se muestran en esta lista:

• O(1): constante. La operación no depende del tamaño de los datos. Es el caso ideal, pero a la vez probablemente el menos frecuente. No se ve en la gráfica de más abajo porque la logarítmica le pasa justo por encima y la tapa.
• O(n): lineal. El tiempo de ejecución es directamente proporcional al tamaño de los datos. Crece en una línea recta.
• O(log n): logarítmica. por regla general se asocia con algoritmos que "trocean" el problema para abordarlo, como por ejemplo una búsqueda binaria.
• O(nlogn): en este caso se trata de funciones similares a las anteriores, pero que rompen el problema en varios trozos por cada elemento, volviendo a recomponer información tras la ejecución de cada "trozo". Por ejemplo, el algoritmo de búsqueda Quicksort.
• O(n²): cuadrática. Es típico de algoritmos que necesitan realizar una iteración por todos los elementos en cada uno de los elementos a procesar. Por ejemplo el algoritmo de ordenación de burbuja. Si tuviese que hacer la iteración más de una vez serían de complejidad O(n³), O(n⁴), etc... pero se trata de casos muy raros y poco optimizados.
• O(2ⁿ): exponencial. Se trata de funciones que duplican su complejidad con cada elemento añadido al procesamiento. Son algoritmos muy raros pues en condiciones normales no debería ser necesario hacer algo así. Un ejemplo sería, por ejemplo, el cálculo recursivo de la serie de Fibonacci, que es muy poco eficiente (se calcula llamándose a sí misma la función con los dos números anteriores: F(n)=F(n-1)+F(n-2)).
• O(n!); explosión combinatoria. Un algoritmo que siga esta complejidad es un algoritmo totalmente fallido. Una explosión combinatoria se dispara de tal manera que cuando el conjunto crece un poco, lo normal es que se considere computacionalmente inviable. Solo se suele dar en algoritmos que tratan de resolver algo por la mera fuerza bruta. No deberías verlo nunca en un software "real".

Podemos verlo gráficamente a continuación (he usado la herramienta gratuita Desmos para graficarlo):

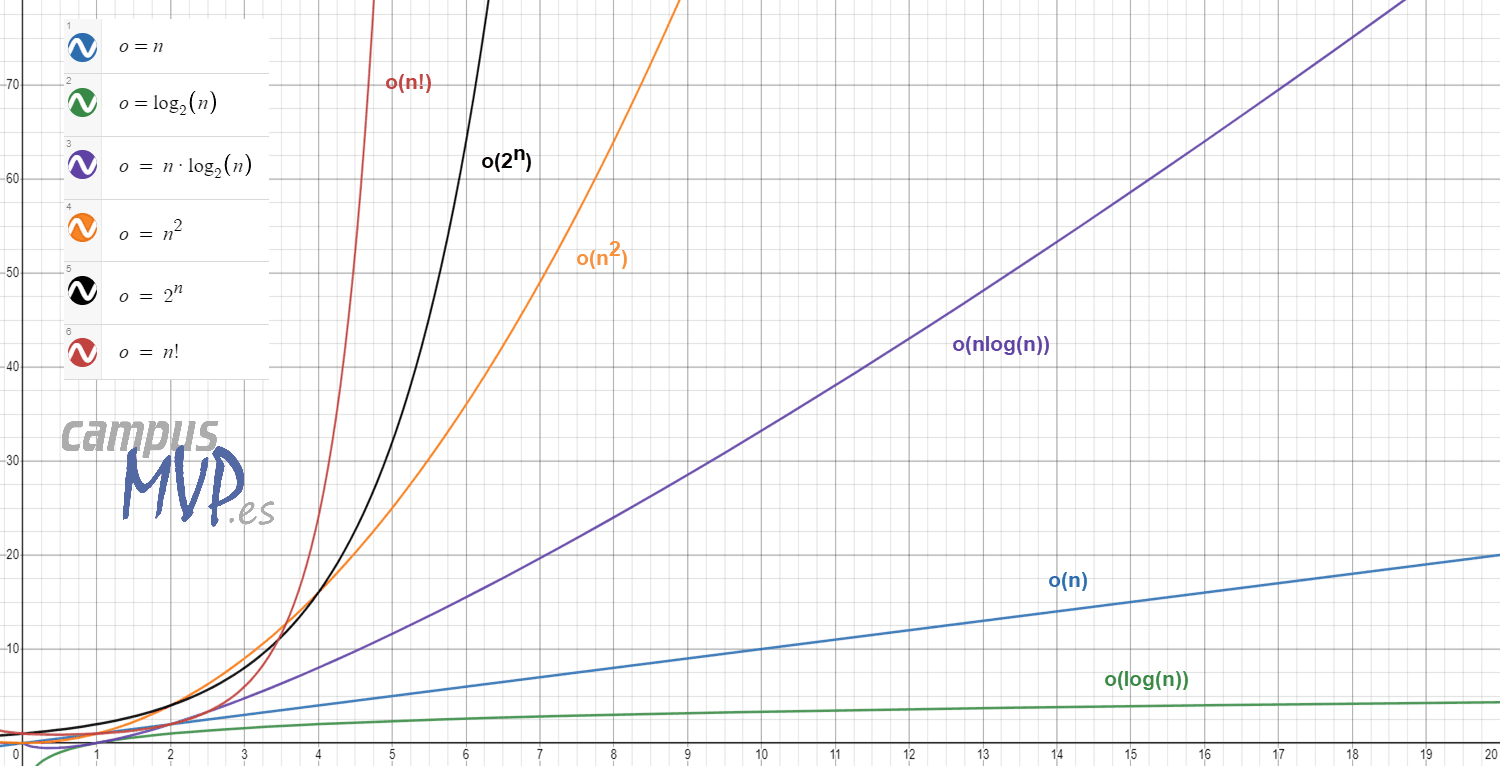
En el eje horizontal tenemos el número de elementos, y en el vertical el tiempo.

Como podemos observar, a medida que aumenta la complejidad, el tiempo necesario para completar la tarea crece mucho, pudiendo llegar a aumentar enormemente en algunos casos en cuanto hay más datos a manejar. Creo que verlo gráficamente es la mejor manera de darse cuenta de su importancia.

Si te encuentras con una función con complejidad cuadrática (O(n²)) o exponencial (O(2ⁿ)) por regla general será señal de que el algoritmo necesita una revisión urgente, y mejor no utilizarlo.

Lo interesante de esta notación es que nos permite comparar varios algoritmos equivalentes sin preocuparnos de hacer pruebas de rendimiento que dependen del hardware utilizado. Es decir, ante resultados equivalentes podemos elegir el algoritmo de mayor rendimiento, que lo será siempre independientemente del hardware si el conjunto de datos es lo suficientemente grande (en conjuntos pequeños un hardware más rápido puede dar resultados más rápidos para un algoritmo menos eficiente, pero a medida que el conjunto crece ya no será así).

Por eso, a partir de ahora, cuando veas que una función documenta explícitamente su complejidad usando la notación Big-O, presta mucha atención y no te olvides de las implicaciones que puede tener en tu aplicación el hecho de utilizarla. Del mismo modo, cuando crees un algoritmo para resolver un problema en tu aplicación, es interesante anotar en la documentación del mismo (aunque sea en los comentarios de la cabecera) cuál es la complejidad algorítmica del mismo en notación Big-O. Eso ayudará a cualquier programador que venga detrás, tanto a usarlo como a tener que optimizarlo, y sabrá cuál es la lógica a batir.

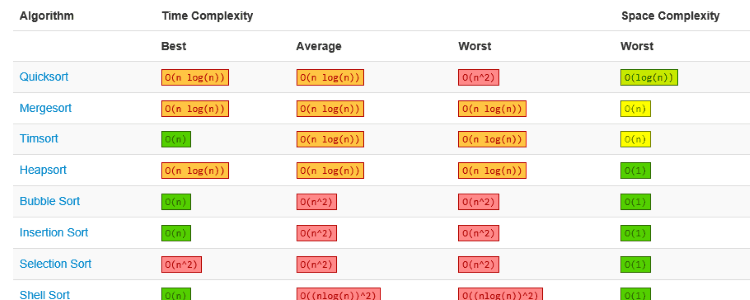
Aquí tienes una tabla muy completa con la complejidad de los principales algoritmos para estructuras de datos, ordenación de matrices, operaciones en grafos y operaciones de montón (heap).

Espero que esta explicación te haya aclarado los conceptos y que no vuelvas a ver la notación Big-O de la misma manera :-)