La recursividad de “cola” (traducción libre de tail recursion) es un mecanismo que permite tener funciones recursivas sin temer por posibles desbordamientos de pila. A diferencia de la recursividad normal, donde cada llamada recursiva implica la creación de un nuevo frame en la pila de llamadas (y por lo tanto el peligro de desbordar el tamaño de la pila), en la tail recursion es posible realizar dichas llamadas recursivas reaprovechando el frame de pila anterior y evitando así el desbordamiento.
Para entender como funciona la tail recursion, antes debemos entender el concepto de Tail Call Optimization (TCO). Para ello vamos a comentar el mismo ejemplo que este de 2ality.com (para más información consulta el enlace, pero te quedará claro más abajo).
Imaginemos el siguiente código JavaScript:
function id(x) {
return x; // Linea (A)
}
function f(a) {
let b = a + 1;
return id(b); // Linea (B)
}
console.log(f(2)); // Linea (C)
En una ejecución normal, sin aplicar TCO, al principio en el frame global de pila tendríamos los valores de id y f (pues estas son las dos variables globales). Sabemos que cuando se llama a una función se crea un frame de pila que contiene los valores de las variables locales y la dirección de retorno. Así pues cuando se llama a la función f dentro del console.log, se crea un frame en la pila de llamadas, con lo que ahora tenemos:
- Frame que contiene los valores locales de f (variables a y b) y la dirección de vuelta (línea C). Este es el top de la pila.
- Frame global
Del mismo modo, cuando dentro de la función f se llama a la función id se crea un tercer frame en la pila de llamadas:
- Frame que contiene los valores locales de id (la variable x) y la dirección de vuelta (línea B). Este es el top de la pila.
- Frame que contiene los valores locales de f (variables a y b) y la dirección de vuelta (línea B).
- Frame global
En este punto (dentro de id) el esquema de la pila sería como el que sigue:
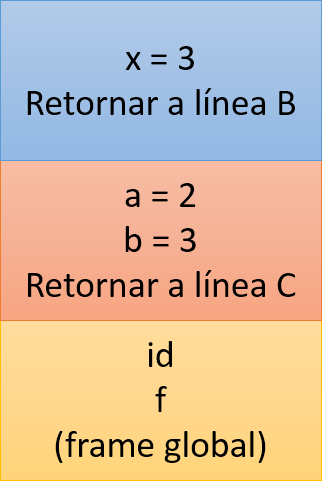
Ahora, una vez termina la llamada a id, el frame azul es eliminado de la pila y posteriormente cuando salimos de f se elimina el frame naranja, quedándonos solo con el frame global. Esta es la situación normal, sin usar TCO: cada llamada a función crea un frame en la pila de llamadas, frame que se elimina cuando se sale de dicha función y se cede el control al llamante de nuevo.
Ahora bien, si nos fijamos en el código podemos deducir que hay un paso que es innecesario. Realmente, todo lo que ocurre en la línea B es el que el valor devuelto por la llamada a id es devuelto a la línea C. Es decir, una vez salimos de id (y volvemos a f) el valor de las variables locales de f ya no lo necesitamos. Llamar a id es lo último que hacemos en f, por lo tanto ¿qué sentido tiene conservar el frame de f en la pila de llamadas si no vamos a necesitarlo para nada más? Imagina que estamos dentro de id pero tenemos la siguiente pila de llamadas:
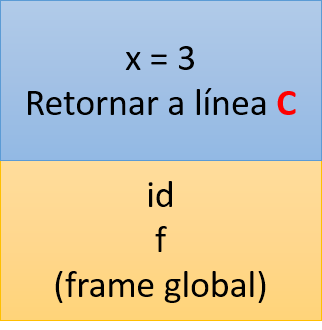
Observa que tenemos en la pila el frame correspondiente a la llamada id y el frame global. Eso sí, hay una modificación en el frame de la llamada a id: en lugar de ceder el control a la línea B (es decir, devolver el control a f), cedemos el control a la línea C. A efectos prácticos el resultado es el mismo que en el caso anterior. Pero hemos conseguido ahorrarnos un frame en la pila. Antes en el peor de los casos teníamos tres, y ahora en el peor de los casos tenemos dos: cuando llamamos a id desde f no creamos un frame nuevo en la pila, si no que sustituimos el frame de f por el de id (modificando la dirección de retorno, eso sí).
Para poder hacer eso es necesaria una condición: que llamar a id sea la última cosa que hagamos en f antes de devolver.
Cuando tenemos una llamada a una función que es lo último que hacemos en otra función, decimos que esta llamada es una tail-call y entonces en este caso, se puede aplicar la tail call optimization y ahorrarnos un frame en la pila de llamadas.
Ahorrarse un frame en la pila de llamadas puede no parecer mucho, pero es muy interesante si somos capaces de crear funciones recursivas, donde la llamada recursiva sea lo último que hagamos. En este caso, se puede aplicar TCO y en lugar de tener un frame de pila por cada llamada recursiva, tendremos uno solo en total. Es el mundo ideal: recursividad sin temer por el desbordamiento. A este tipo de recursividad la conocemos como tail recursion (o recursividad de “cola”). Veamos un ejemplo de ella.
Vamos a partir de una función recursiva clásica. En este caso el factorial:
function fact(n) {
if (n == 0)
return 1 ;
else
return n * fact(n-1) ;
}
Esta función recursiva es básicamente la misma que la del artículo anterior, dedicado a la recursividad. Es un ejemplo de recursividad clásica.
Veamos ahora como quedaría el mismo ejemplo usando tail recursion:
function fact(n) {
return tail_fact(n,1) ;
}
function tail_fact(n,a) {
if (n == 0)
return a ;
else
return tail_fact(n-1,n*a) ;
}
La diferencia entre la función fact recursiva original y la tail_fact es que en la primera no podemos aplicar TCO por qué realmente llamar a fact desde fact no es la última cosa que hacemos. Puede parecer que sí, leyendo el código, pero no es cierto. Observa que antes de devolver, multiplicamos el valor por n. Por lo tanto debemos tener este valor de n accesible y este valor está en el frame correspondiente, y en cada frame el valor de n es distinto, por lo que necesitamos mantener todos esos valores de n porque debemos recuperarlos al ir “deshaciendo” la recursividad.
Por otro lado tail_fact lo último que hace antes de devolver es... llamar a tail_fact. No multiplica el valor de tail_fact por una variable local (como si hace fact), por lo tanto el estadio intermedio de todos los saltos recursivos no lo necesitamos para nada.
Aplicando TCO, incluso si llamases a fact(10000) terminarías teniendo tres frames en la pila: el global, el de la función fact y el de la función tail_fact. En cambio con la versión recursiva tradicional tendrías 10001 frames en la pila, y muy probablemente un desbordamiento.
Por supuesto para usar TCO es necesario que nuestro código use tail recursion pero también que el compilador o motor del lenguaje lo soporte. P. ej. Scheme obliga a que todas las implementaciones soporten TCO y lo mismo ocurre en… ¡ECMAScript 2015!
¡Espero que te haya resultado interesante!