Un concepto que siempre le cuesta bastante a los programadores que están empezando es el de recursión o recursividad (se puede decir de las dos maneras).
Aunque es un concepto que puede llegar a ser muy complejo, en esencia es muy sencillo:
La recursividad consiste en funciones que se llaman a sí mismas, evitando el uso de bucles y otros iteradores.
Un ejemplo fácil de ver y que se usa a menudo es el cálculo del factorial de un número entero. El factorial de un número se define como ese número multiplicado por el anterior, éste por el anterior, y así sucesivamente hasta llegar a 1. Así, por ejemplo, el factorial del número 5 sería: 5x4x3x2x1 = 120.
Tomando el factorial como base para un ejemplo, ¿cómo podemos crear una función que calcule el factorial de un número? Bueno, existen multitud de formas. La más obvia quizá sería simplemente usar un bucle determinado para hacerlo, algo así en JavaScript:
function factorial(n){
var res = 1;
for(var i=n; i>=1; i--){
res = res * i;
}
return res;
}
Sin embargo hay otra forma de hacerlo sin necesidad de usar ninguna estructura de bucle que es mediante recursividad. Esta versión de la función hace exactamente lo mismo, pero es más corta, más simple y más elegante:
function factorial(n) {
if (n<=1) return 1;
return n* factorial(n-1);
}
Aquí lo que se hace es que la función se llama a sí misma (eso es recursividad), y deja de llamarse cuando se cumple la condición de parada: en este caso que el argumento sea menor o igual que 1 (que es lo que hay en el condicional).
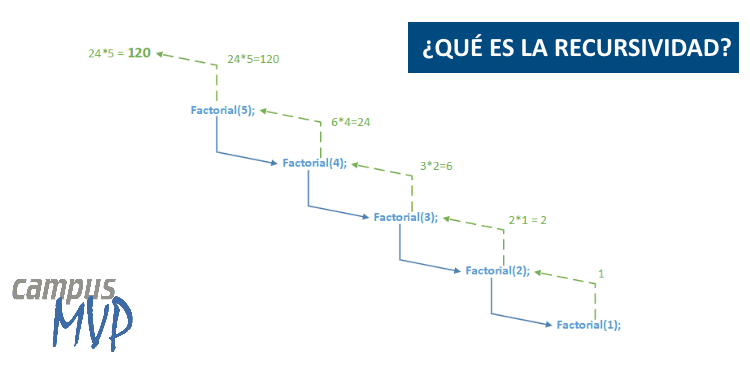
Si analizamos su ejecución paso a paso veríamos lo que está representado por la siguiente animación:
Es decir, cuando llamamos a la primera función, ésta se llama a sí misma pero pasándole un número menos y así sucesivamente hasta llegar a la última (la que recibe un 1 y por lo tanto deja de hacer más llamadas). En el momento en el que alguna de ellas empieza a devolver valores "hacia atrás", regresa la llamada a cada una de ellas, los valores devueltos se van multiplicando por el parámetro original en cada una de ellas, hasta llegar arriba del todo en el que la primera llamada devuelve el valor buscado.
Es un concepto que cuesta un poco entender pero que es muy poderoso.
Ventajas e inconvenientes
¿Ganamos algo al utilizar recursión en lugar de bucles/iteradores para casos como este?
En este caso concreto del cálculo factorial no, y de hecho es una forma más lenta de hacerlo y ocupa más memoria. Esto no es preocupante en la realidad, pero conviene saberlo. Lo del factorial es solo una forma de explicarlo con un ejemplo sencillo y que sea fácil de entender.
Pero entonces, si no ganamos nada en este caso ¿para qué sirve realmente la recursividad?
Pues para resolver ciertos problemas de manera elegante y eficiente.
El ejemplo típico sería el recorrer un árbol de elementos para hacer algo con todos ellos. Imagínate un sistema de archivos con carpetas y subcarpetas y archivos dentro de estas carpetas, o el árbol de elementos (DOM) de una página web donde unos elementos incluyen a su vez otros y no sabes cuántos hay en cada uno. En este tipo de situaciones la manera más eficiente de hacer una función que recorra todos los elementos es mediante recursión. Es decir, creas una función que recorra todos los elementos hijo del nodo que le pases y que se llame a sí misma para hacer lo mismo con los sub-nodos que haya. En el caso del sistema de archivos le pasarías una carpeta y se llamaría a sí misma por cada subcarpeta que hubiese, y así sucesivamente con todas las demás. Con una sola llamada inicial recorrerá automáticamente toda la estructura del sistema de archivos.
Con eso, y sin necesidad de complicarte, de repente tienes una función muy poderosa capaz de enumerar cualquier estructura arbitraria por compleja que sea.
Ahí es donde se ve el verdadero poder de la recursividad, aunque hay aplicaciones más potentes y más complejas todavía.
Detalles a tener en cuenta
Otra cosa importante a tener en cuenta es que, cada vez que se hace una llamada a una función desde otra función (aunque sea a sí misma), se crea una nueva entrada en la pila de llamadas del intérprete. Ésta tiene un espacio limitado por lo que puede llegar un punto en el que si se hacen demasiadas se sature y se produzca un error. A este error se le denomina "Desbordamiento de pila" o "Stack Overflow". Ahora ya sabes de donde viene el nombre del famoso sitio para dudas de programadores sin el que la programación moderna no sería posible ;-)
Además, hay que tener mucho cuidado con la condición de parada. Ésta se refiere a la condición que se debe comprobar para determinar que ya no se harán más llamadas a la función. Es en ese momento en el que empiezan a devolverse los valores hacia "arriba", retornando a la llamada original.
Si no tienes la condición de parada controlada pueden pasar varias cosas (todas malas), como por ejemplo:
- Que se sature la pila y se produzca un desbordamiento
- Que ocupes cada vez más memoria
- Que se produzcan desbordamientos de variables al ir acumulando resultados
- En JavaScript, que el navegador -al cabo de unos segundos- avise al usuario de que hay un script descontrolado y que lo detenga.
- ....
Así que es crucial controlar la condición de parada.
Por ejemplo, en el caso de nuestro cálculo factorial en JavaScript, como esta función enseguida crea números enormes, es bueno que lo limitemos de algún modo. En este caso sencillo del factorial, por ejemplo podríamos limitar el cálculo al número 100 (¡100 factorial es enorme!, un valor seguido de cientos de ceros) y así limitamos el número de llamadas en la pila a 100 como máximo también. Además, ya que estamos, le añadimos soporte para que calcule factoriales de números negativos.
Para ello podemos tener esta versión "definitiva" de la función recursiva:
function factorial(n) {
n = parseInt(n); //Trato de obtener un entero
var signo = Math.sign(n); //Averiguo su signo
n = Math.abs(n); //Calculo el factorial sobre el valor absoluto (positivo)
if (n>=100)
throw "El número es demasiado grande;";
//Cálculo del factorial
if (isNaN(n) || n<=0) return 1;
return signo*n* factorial(n-1); //Se devuelve el signo (solo en la primera llamada habrá signo negativo)
}
Que usa igualmente recursión, pero le hemos metido otro tipo de controles para hacerla más robusta.
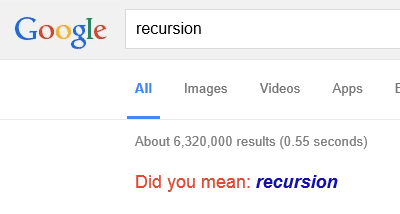
Como nota simpática sobre la recursión: si buscas en Google (en inglés) la palabra "Recursion" (que es recursividad en inglés) te dice que si querías decir "Recursion" (o sea, lo mismo), en un guiño a los programadores que saben qué significa esto  :
:
¡Espero que te resulte útil!